The Coulomb Train Model (CTM) is a straightforward, easily pictured representation that helps novice learners develop an initial “sense of mechanism” about how electric circuits work. You can read about it here and here (and, to some extent, track its development over time).

In this post, however, I want to focus on how effective the CTM is in helping students understand the energy and power formulas associated with electric circuits: notably E = QV, P = IV and P=I²R.

E=QV and the CTM

The E in E=QV stands for the energy transferred to the bulb by the electric current (in joules, J). The Q is the charge flow in coulombs, C. The V is the potential difference across the resistor in volts, V.

Using the Coulomb Train Model:

• Each grey truck passing through the bulb represents one coulomb of charge flow. Q is therefore the number of grey trucks passing through the bulb in a certain time t. (We won’t specify what that time t is now but we will return to it shortly.)
• The potential difference V is the energy transferred out of each coulomb as they pass through the bulb. If one joule (represented by the orange stuff in the truck) is transferred from each coulomb then the potential difference is one volt. If two joules then the potential difference is two volts, and so on.

How can we increase the energy transferred into the bulb? There are two ways:

1. Increase the total number of coulombs passing through the bulb. That is to say, increasing Q. We could do this by (a) waiting a longer time so that more coulombs pass through the bulb; or (b) increasing the current so that more coulombs pass through each second.
2. Increase the energy transferred from each coulomb into the bulb. That is to say, increasing V. We could do this by increasing the potential difference of the cell so that each coulomb is loaded up with more energy.

Or, of course, we could increase the values of Q and V simultaneously.

All you need is E = Q V

In other words, the energy transferred per second (or the power P in watts, W) is equal to the product of the current I in amperes (or coulombs per second) and the potential difference V in volts, V.

A higher current will increase the power transferred to the bulb: more coulombs will pass through the bulb per second so more energy is transferred to the bulb each second. This can be modelled using the Coulomb Train Model as shown:

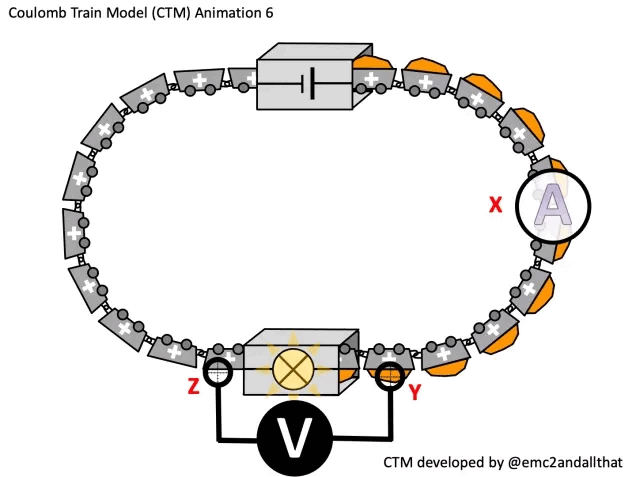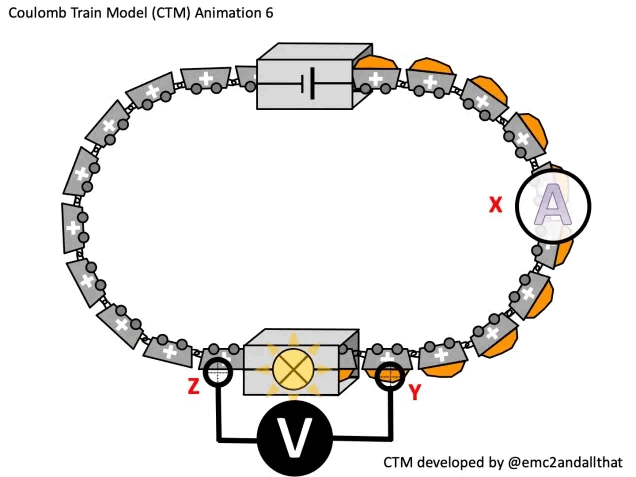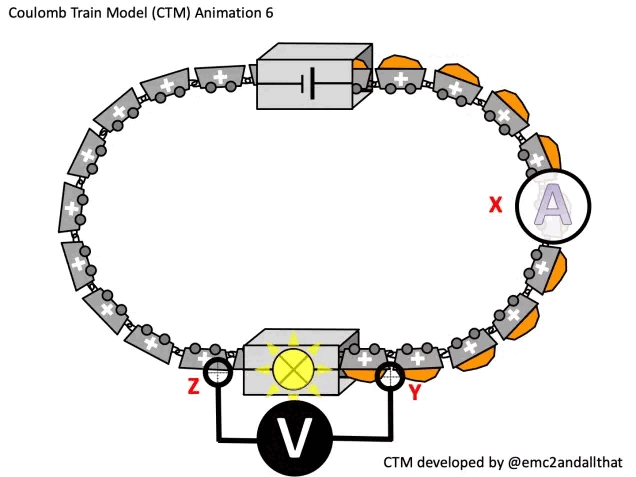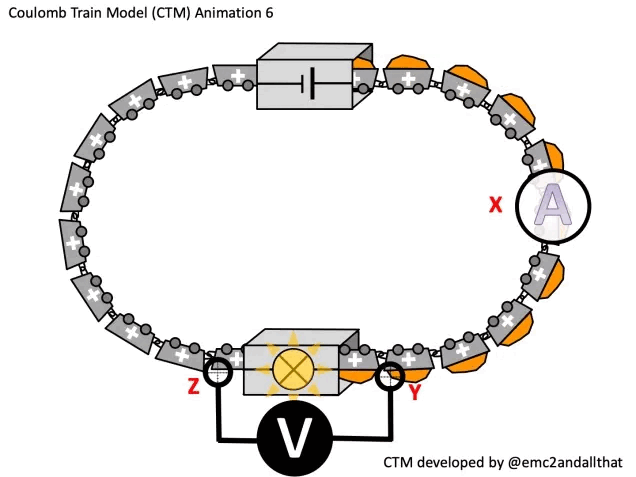
Increasing the potential difference V (i.e. the energy carried by each coulomb) would also increase P.

Deriving P=I²R from P=IV

If we start with P=IV but remember that V=IR then P=I(IR) so P=I²R.

This can be represented on the Coulomb Train Model like this:

We can increase the power transferred to the resistor by:

• Increasing the value of the resistor (and keeping I constant, which implies that V would have to be increased). Doubling the value of R would double the value of P.
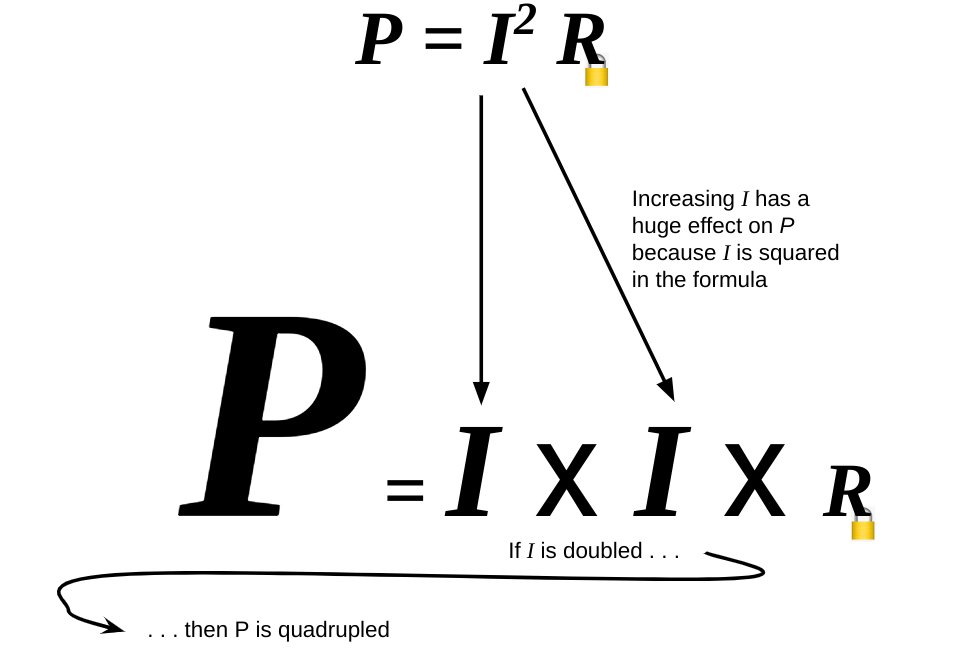
• Increasing the value of I. However, since the formula includes I squared then this would have a disproportionate effect on P. For example, if I was doubled then P would be quadrupled. A Hewitt representation can be useful for highlighting this to students; for example:

Linking the electrical power formulas

The electrical power equations when considered in isolation can seem random and unconnected. Making the links between them explicit can be not just a powerful aid to memory, but also hints at the power and coherence of that noble exploration of reality and possibility called physics.