Forces

Forces and Inclined Planes

e=mc2andallthat2 Comments

I don’t want to turn the world upside down — I just want to make it a little bit tilty.

In this post, I want to look at the physics of inclined planes, as this is a topic that can trip up students at GCSE and A-level. I believe that one of the reasons for this is that students often have only a fuzzy notion of what we mean by ‘vertical’ and ‘perpendicular’. These terms are often treated as synonymous so I think they could do with some unpicking.

The absolute vertical

The absolute vertical anywhere on the Earth surface is defined by the direction of the Earth’s gravitational field. It will be a radial line connected with the centre of mass of the planet. The direction of the absolute vertical will be shown by line of a plumb line as shown in the diagram.

Using plumb lines to identify the line of the absolute vertical

(As a short aside, A and B indicate why the towers of the Humber Bridge are 3.6 cm further apart at the top than they are at the bottom. Take that, flat-earthers!)

Picture from https://commons.wikimedia.org/wiki/File:Humber_Bridge_From_Air.jpg

The local perpendicular

We define the local perpendicular as a line which is at 90o to the plane or surface or table top we are working on. We can find its direction with a set square as shown in the picture below.

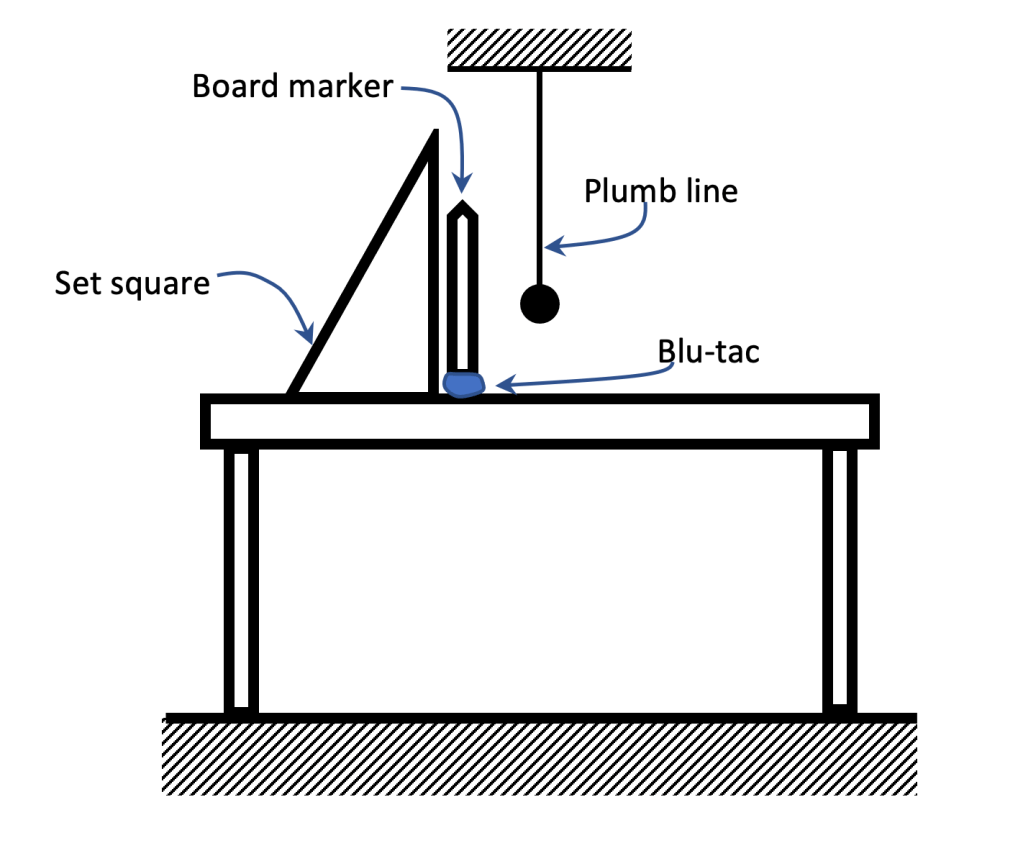
Example of when the local perpendicular is aligned with the absolute vertical

Next we tilt the table so that the local perpendicular and absolute vertical are no longer aligned. (Thanks to my colleague Bruce Pawsey for this idea.)

Example of the local perpendicular and the absolute vertical no longer in alignment.

Forces on a dynamics trolley on an inclined plane (GCSE level analysis)

Next we place a dynamics trolley on a horizontal table top. We observe that it is is equilibrium. This is easy to explain if we draw a free body diagram to show the forces on the trolley.

The forces on a trolley on a horizontal surface

The normal reaction force N on the trolley is equal and opposite to the weight W of the trolley. The resultant (total) force on the trolley is zero so it is not accelerating.

But now note what happens if we tilt the table so that it becomes an inclined plane: the trolley accelerates to the left.

At GCSE, it is probably best to restrict the analysis to what happens in the absolute vertical (shown by the plumb line) and the absolute horizontal (at 90o to the plumb line).

If we resolve the normal reaction force into two components, we see that N has a small horizontal component (see above). This is the resultant force that causes the trolley to accelerate to the left as shown.

Forces on an object on an inclined plane (A level analysis for static equilibrium)

If we flip the trolley so that it is upside down, then there will be a frictional force acting parallel to the slope. This means that, as long as the angle of tilt is not too steep, the object will be in equilibrium.

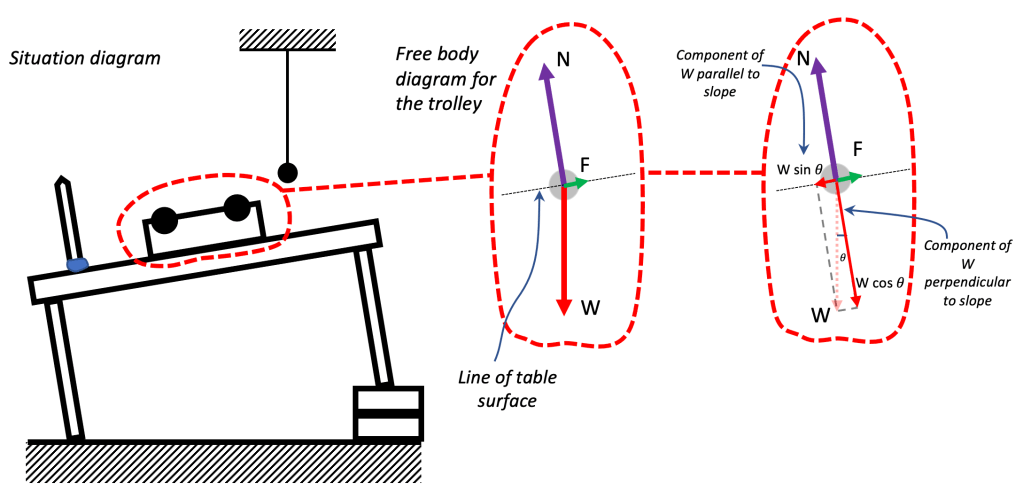
It now makes sense to resolve W into components parallel and perpendicular to the slope, since it is the only force of the three which is aligned with the absolute vertical. F and W are aligned with the local perpendicular and horizontal to it’s less onerous to use these as the ‘reference’ grid in this instance.

The normal reaction force N is equal to W cos 𝜃 not W and since cos 𝜃 is always less than 1 (for angles other than 90o). If we placed the trolley on some digital scales then the reading on the scales would decrease as we increased 𝜃.

This effect was used to simulate the lower gravitational field strength on the Moon for training astronauts for the Apollo programme. In effect, they trained on an inclined plane. (‘To attain the Moon’s terrain / One trains mainly on an inclined plane.‘)

If the wheels of the trolley were in contact with the table surface so that the frictional force were negligible, then the trolley would accelerate down the slope because of the resultant force of W sin 𝜃 parallel to the slope. The direction of the acceleration is parallel to the slope (i.e. at 90o to the local perpendicular) and not along the absolute horizontal as suggested by the earlier, simpler GCSE-level analysis in the previous section.

The Acceleration Required Practical Without Light Gates PART DEUX

e=mc2andallthat5 Comments

I have written about completing the acceleration practical without light gates before but I thought I’d share a slight variation on the original method that I have found to work well with my teaching groups. Links to some digital resources (spreadsheet, powerpoint and worksheet) will be included.

The method does not require light gates or a data logger. In fact, the only measuring instruments needed are a metre rule and a stop clock. The other items are standard laboratory equipment (dynamic trolley, bench pulley, string. 4 x 10 g masses on a hanger, 4 x 100 g masses on a hanger, and wooden runway). If your class can access IT then a rather clever spreadsheet is included, but this is not essential.

We use small 10 g masses to accelerate the trolley so the time it takes to travel a certain distance (between 0.50 to 0.90 m) can be timed manually with a stop clock (typical time for the 10 g mass is between 3 and 5 seconds).

This works well as a class practical, especially if you follow Adam Boxer’s excellent ‘Slow Practical’ method.

The Powerpoint that I use to run this practical can be downloaded here.

Set up a friction-compensated slope

The F in Newton’s Second Law stands for the resultant force (or total force) so ideally we should eliminate any frictional force tending to slow down the trolley. This can be done by tilting the runway slightly as shown.

Using one or two 100 g slotted masses propped under one end of the runway provides enough of a slope so that the trolley continues moving at a steady speed when given a short, gentle push. Use trial and error to find the precise angle of the slope needed.

Students should mark START and STOP lines on the runway and measure the distance s between them and record it on the worksheet (or in the spreadsheet).

Make sure the weight stack does not hit the ground before the trolley crosses the stop line, otherwise the results will be unreliable as the trolley will not be accelerating over the full distance.

Use a system of constant mass

Increase the mass of the trolley, but keep F fixed

Calculate the acceleration

The force of the weight stack on the trolley can be calculated using W=mg where m is the mass in kilograms and g is the gravitational field strength of 9.81 N/kg, although the approximation 10 g = 0.10 N can be useful if students are performing the calculations and plotting the graph manually.

Students can use the formula a = 2s/t2 to calculate the acceleration manually. Note that the units of this expression are m/s2 as we would expect for a valid equation for acceleration.

A derivation of this expression suitable for GCSE students is outlined on Slide 5 of the Powerpoint.

If students have access to tablets or computers, they can use this spreadsheet to automatically calculate the results and plot the graph. Students can print the graph if they click on the relevant tab. (The line of best fit is not included as all students generally benefit from practicing this skill!)

Evaluate the results

Students can evaluate the results using Slide 7 of the Powerpoint.

Note that in the graph shown, although there is a convincing straight line of best fit, there is also a noticeable systematic error: the acceleration is slightly too small for the indicated force. This would suggest that the runway was not tilted steeply enough to eliminate all frictional forces.

If you find this blog and resources useful, please leave a comment and/or share it on Twitter 🙂

Keep Calm and Draw Free Body Force Diagrams (Part 2)

e=mc2andallthat8 Comments

You can read Part 1 which introduces the idea of free body force diagrams here.

Essentially the technique we will use is as follows:

  1. Draw a situation diagram with NO FORCE ARROWS.
  2. ‘Now let’s look at the forces acting on just object 1’ and draw a separate free body diagram (i.e. a diagram showing just object 1 and the forces acting on it)
  3. Repeat step 2 for some or all of the other objects at your discretion.
  4. (Optional) Link all the diagrams with dotted lines to emphasise that they are facets of a more complex, nuanced whole

The Wheel Thing

Let’s consider a car travelling at a constant velocity of 20 miles per hour.

NOT a force diagram. (Note: whilst force arrows on situation diagrams should be discouraged, there is no equivalent argument for speed arrows)

’20 m.p.h.’ is such an uncivilised unit so let’s use the FIFA system to change it into more civilised scientific S.I. units:

NOT a force diagram! (Note: it is fine to draw speed/velocity/acceleration arrows on a situation diagram, but not force arrows.)

Note that point A on the car tyre is moving at 8.9 m/s due to the rotation of the wheel, as well as moving at 8.9 m/s with the rest of the car. This means that point A is moving at 8.9 + 8.9 = 17.8 m/s relative to the ground.

More strangely, point B on the car tyre is moving backwards at speed of 8.9 m/s due to the rotation of the wheel, as well as moving forwards at 8.9 m/s with the rest of the car. Point B is therefore momentarily stationary with respect to the ground.

The tyres can therefore ‘grip’ the road surface because the contact points on each tyre are stationary with respect to the road surface for the moment that they are in position B. If this was not the case, then the car would be difficult to control as it would be in a skid.

(Apologies for emphasising this point — I personally find it incredibly counterintuitive! Who says wheels are not technologically advanced!)

Forces on a tyre

Situation diagram (note: no force arrows) and free body diagrams for road and tyre. Note also different style of arrow for speed and force.

Assuming the car in the diagram is a four wheel drive, the total force driving it forward would be 4 x 330 N = 1320 N. Since it is travelling at a constant speed, this means that there is zero resultant force (or total force). We can therefore infer that the total resistive force acting on the car is 1320 N.

It is can also be slightly disconcerting that the force driving the car forward is a frictional force because we usually speak of frictional forces having a tendency to ‘oppose motion’.

And so they are in this case also. The movement they are opposing is the relative motion between the tyre surface and the road. Reduce the frictional force between the road with oil or mud, and the tyre would not ‘lock’ on the surface and instead would ‘spin’ in place. It’s worth bearing in mind (and communicating to students) that the tread pattern on the tyre is designed to maximise the frictional force between the tyre surface and the road

And then a step to the right…

It’s just a jump to the left

And then a step to the right

The Time Warp, Rocky Horror Picture Show
Situation diagram for a person taking a step to the right; and free body diagrams for the person and the floor

We can see how important friction is for taking a step forward in the above diagrams. Again, it is worth pointing out to students how much effort goes into designing the ‘tread’ on certain types of footwear so as to maximise the frictional force. On climbing boots, the ‘tread’ extends on to the upper surface of the boot for that very reason.

Amazon.com | La Sportiva Men's TC Pro Climbing Shoe | Climbing
A climbing boot

One step beyond

Let’s apply a similar analysis to the case of a person stepping off a boat that happens not be tied to the mooring.

Situation diagram for a person stepping off an unmoored boat; and free body force diagrams for the person and the boat. Note different style of arrow for forces and acceleration.

The person pushes back on the boat (gripping the boat with friction as above). By Newton’s Third Law, this generates an equal an opposite force on the boat. There is no horizontal force to the right due to the tension in the rope, since there is no rope(!) This means that there is a resultant force on the boat to the left so the boat accelerates to the left.

The forces on the person and the boat will be equal in magnitude, but the acceleration will depend on the mass of each object from F = ma.

Since the boat (e.g. a rowing boat) is likely to have a smaller mass than the person, its acceleration to the left will be higher in magnitude than the acceleration of the person to the right — which will lead to the unfortunate consequence shown below.

The effect of stepping off an unmoored boat

The acceleration of the person and the boat happens only when the person and boat are in contact with each other, since this is the only time when there will be a resultant force in the horizontal direction.

Note that although force arrows on a situation diagram should be discouraged for the sake of clarity, there is an argument for drawing velocity and acceleration arrows on the situation diagram as a form of dual coding. Further details can be found here, and an explanation of why acceleration is shown as a double headed arrow.

The velocity to the left built up by the boat in this short instant will be greater than the velocity to the right built up by the person, because the acceleration of the boat is greater, as argued above.

The outcome, of course, is that the person falls in the water, which has been the subject of countless You’ve Been Framed clips.

Next post…

In the next post, I will try to move beyond horizontal forces and take account of the normal reaction force when an object rests on both horizontal surfaces and inclined surfaces.

Fear of Forces? Keep Calm and Draw Free Body Diagrams

e=mc2andallthat2 Comments

Why do so many students hold pernicious and persistent misconceptions about forces?

Partly, I think, because of the apparent clash between our intuitive, gut-level knowledge of real world physics. For example, a typical student might find the statement ‘If I push this box, it will stop moving shortly after I stop pushing because force is needed to move things‘ entirely unobjectionable; whilst in the theoretical, rarefied world of the physicist the statement ‘The box will keep moving at a constant velocity after I stop pushing it, unless it is acted on by a resultant force such as friction‘ would get a tick whereas the former would get a big angry X and and a darkly muttered comment about ‘bloody Aristotleans.’

After all, ‘pernicious’ is in the eye of the beholder. Physics teachers have to remember that they suffer mightily under the ‘curse of knowledge’ and have forgotten what it’s like to look at the world through anything than the lens of Newtonian mechanics.

We learn about the world through the power of example. Human beings are ‘inference engines’: we strive to make sense of the world by constructing general rules based on the examples presented to us.

Many of the examples of forces in action presented to students are in the form of force diagrams; and in my experience, all too many force diagrams add to students’ confusion.

A bad force diagram

Force Diagram 1: version 1 (really bad)

Over the years, I have seen many versions of this diagram. To my own chagrin, I must admit that I, personally, have drawn versions of this diagram in the past. But I now recognise it has one major, irredeemable flaw: the arrows are drawn hanging in mid-air.

OK, let’s address this. Is this better?

Force Diagram 1: version 2 (still bad)

No, it isn’t because it is still unclear which forces are acting on which object. Is the blue 75 N arrow the person pushing the cart forward or the cart pulling the person forward? Is the red 75 N arrow the cart pushing back on the person or the person pulling back on the cart?

From both versions of this diagram shown above: we simply cannot tell.

As a consequence, I think the explanatory value of this diagram is limited.

Free Body Diagrams to the Rescue!

A free body diagram is simply one where we consider the forces on each object in the situation in turn.

Force Diagram 1: version 3 (much better!)

We begin with a situation diagram. This shows the relationship between the objects we are considering. Next, we draw a free body diagram for each object; that is, we draw each object involved and consider the forces acting on it.

From version 3 of Force Diagram 1, we can see that it was an attempt to illustrate Newton’s Third Law i.e. that if body A exerts a force on body B then body B exerts an equal and opposite force on body A.

Another bad force diagram

Force Diagram 2: version 1 (very bad)

This is a bad force diagram because it is unclear which forces are acting on the cart and which are acting on the person. Apart from a very general ‘Well, 50 N minus 50 N means zero resultant force so zero acceleration’, there is not a lot of information that can be extracted from this diagram.

Also, the most likely mechanism to produce the red retarding force of 50 N is friction between the wheels of the cart and the ground (and note that since the cart is being pushed by an external body and the wheels are not powered like those of a car, the frictional force opposes the motion). Showing this force acting on the handle of the cart is not helpful, in my opinion.

Free body diagrams to the rescue (again)!

The Newton 3 pairs are colour coded. For example, the orange 50 N forward force on the person (object A) is produced as a direct result of Newton’s 3rd Law because the person’s foot is using friction to grip the floor surface (object B) and push backwards on it (the orange arrow in the bottom diagram).

This diagram shows a complete free body diagram body analysis for all three objects (cart, person, floor) involved in this simple interaction.

I’m not suggesting that all three free body diagrams always need to be discussed. For example, at KS3 the discussion might be limited at the teacher’s discretion to the top ‘Forces on Cart’ diagram as an example of Newton’s First Law in action. Or equally, the teacher may wish to extend the analysis to include the second and third diagrams, depending on their own judgement of their students’ understanding. The Key Stage ticks and crosses on the diagram are indicative suggestions only.

At KS3 and KS4, there is not a pressing need to explicitly label this technique as ‘free body force diagrams’. Instead, what I suggest (perhaps after drawing the situation diagram without any force arrows on it) is the simple statement that ‘OK, let’s look at the forces acting on just the cart’ before drawing the top diagram. Further diagrams can be introduced with a similar statements such as ‘Next, let’s look at the forces acting on just the person’ and so on. Linking the diagrams with dotted lines as shown is, I think, useful in not losing sight of the fact that we are dealing piecemeal with a complex and nuanced whole.

Conclusion

The free body force diagram technique (whether or not the teacher decides to explicitly call it that) offers a useful tool that will allow us all to (fingers crossed!) draw better force diagrams.

  1. Draw a situation diagram with NO FORCE ARROWS.
  2. ‘Now let’s look at the forces acting on just object 1’ and draw a separate free body diagram (i.e. a diagram showing just object 1 and the forces acting on it)
  3. Repeat step 2 for some or all of the other objects at your discretion.
  4. (Optional) Link all the diagrams with dotted lines to emphasise that they are facets of a more complex, nuanced whole

In the next post, I hope to show how the technique can be used to explain common problems such as how a car tyre interacts with the ground to drive a car forward.

You can read Part 2 here.